Maths Sample Paper 5, Part - A for class 10th
Maths Sample Paper
Part - A (28 marks)
Section - I (1 marks each)
1. Find the number of terms from 1 to 1000 which is divisible by 7.
2. If (4 - k)x² + 2(k+2)x + (8k+1) =0 has equal roots, then find the value of k.
Or
If x = 1/2 is a root of the equation x² + kx -5/4 = 0, then find the value of k.
3. The perimeter of two similar triangles ABC and PQR are respectively, 48cm and 36cm. If PQ= 12cm, then find AB.
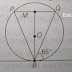
4. In the given figure, if ABC is the tangent to a circle at B whose centre is O, PQ is a chord to AC and angle QBC =65°, then find the value of angle PBQ.
Or
If PT is a tangent at T to a circle, where centre is O and OP =17cm, OT = 8cm, then find the length of the tangent segment PT.
5. In a ∆ABC, right angled at B, if base line is AB=12 and BC=5, then determine the cos C.
You are watching this Sample Paper on
Educbse - The platform of learning
6. Find the altitude of an equilateral triangle having the length of its side 10 cm.
7. In a circle of radius 21cm, an arc subtends an angle of 60° at the centre, then find the length of the arc.
8. By melting a solid cylinderical metal, a few conical materials are to be made. If three times the radius of the cone is equal to twice the radius of the cylinder and the ratio of the height of the cylinder and the height of the cone is 4 : 3, then find the number of cones which can be made.
9. If a dice is thrown once, there are two possible outcomes getting a number greater than 4 as less than equal to 4. Find the probability of getting a number greater than 4.
10. Find the value of
2 sin² 30° tan60° - 3cos²60°
Or
From a point on the ground, the angle of elevation of the bottom and top of a transmission tower fixed at the top of a 20m high building are 45° and 60°, respectively. Find the height of the tower.
11. Is this statement true?
If discriminant of a quadratic polynomial is equal to zero, then graph (parabola) represented by it touches.
12. If the probability that it will rain tomorrow is 0.75, then find the probability that it will not rain tomorrow.
13. Find the 25th term of the AP -5, -5/2, 0, 5/2
Or
Determine the AP whose third term is 5 and the 7th term is 9.
14. If angle between two tangents drawn from a point P to a circle of radius A and centre O is 90°, then find the value of OP.
15. If AB is a tangent drawn from a point A to a circle with centre O and BOC is a diameter of the circle such that angle AOC =120°, then find angle OAB.
16. If tan∅ = 1/2,then find the value of
2cot²∅ + 2
Or
Eliminate ∅ from x = a+b sec∅, y = c + d tan∅.
Section- II (4 marks each)
17. Case Study I
200m Race
A Rafree is standing on the side of the athletic track and kept a stopwatch, which is used to find the time that it took a group of students to run 200m.
In different time intervals, different number of students completed the race are given in the table as shown below
Time 0-50 50-100 100-150 150-200
Number of 10 15 7 8
Students.
a) Find the average time taken to complete 200m race.
i. 90.50s
ii. 91.25s
iii. 92s
iv. 93s
b) With the help of histogram, which measurement can be determined.
i. Mean
ii. Mode
iii. Median
iv. None of these
c) Find the mode of the given data
i. 59.62
ii. 58.30
iii. 58.50
iv. 59.98
d) Find the lower limit of the median class.
i. 25
ii. 75
iii. 100
iv. 50
e) Find the number of students, who have finished the race after 100s.
i. 14
ii. 15
iii. 30
iv. 25
18. Case study II
No Smoking Campaign
All of thems know that smoking is injurious for health. So, college students decide to make a campaign.
To raise social awareness about hazards of smoking, a school decided to start "No Smoking" campaign. 10 students are asked to prepare campaign banners in the shape of triangle as shown in figure
a) If the cost of per square centimetre of banner is RS 2, then find the overall cost incurred on such campaign.
i. Rs 200
ii. Rs 180
iii. Rs 190
iv. Rs 210
b) Which mathematical concept is used in this question.
i. Area of triangle
ii. Prime factorization method
iii. Arithmetic progression
iv. None of the above.
c) If we want to draw a circumscribed circle of given, then find the coordinate of the centre of circle.
i. (3.5, 3)
ii. (3, 3)
iii. (4.5, 3)
iv. (3, 3.5)
d) If we draw the image of figure about the line BC, then total area will be
i. 18
ii. 20
iii. 22
iv. 24
e) Find the centroid of the given triangle.
i. (8/3, 7/3)
ii. (4, 3.5)
iii. (7/3, 8/3)
iv. None of these
19. Case Study III
Book seller
A book seller has 420 science stream books and 130 Arts stream books. He wants to stack them in such a way that each stack has the same number and they take up the least area of the surface.
a) If a number has no factors other than 1 and number itself is
i. Composite
ii. Prime
iii. Don't say anything
iv. None of the above
b) What is the maximum number of books that can be placed in each stack for this purpose?
i. 10
ii. 14
iii. 12
iv. 15
c) Which mathematical concept is used to solve the problem?
i. Prime factorisation method
ii. Area of triangle
iii. Arithmetic progression
iv. None of the above
d) If the book seller double the quantity, then the maximum number of books that can be placed in each stack is
i. Remain same
ii. Double
iii. Triple
iv. None of these
e) Find the LCM of the given book streams.
i. 5450
ii. 5460
iii. 2730
iv. None of these
You are watching this Sample Paper on
Educbse - The platform of learning
Thanks for watching
Posted by :- Anuranjan Gadekar






No comments